Pedigree collapse is an advanced but important genetic genealogy topic. This first part of a two-part article explains how pedigree collapse plays into the DNA matching experience.

Have you ever thought about how many ancestors you have? To start with you have 2 parents, then 4 grandparents, 8 great-grandparents, 16 gg-grandparents, 32 ggg-grandparents, 64 gggg-grandparents, and so forth. Your pedigree starts with you at the point of an inverted triangle that fans out, doubling the number of ancestors at each generation.

By the time you get out to 10 generations there are 1,024 spots for ancestors on your pedigree chart, and the numbers just keep doubling from there. Pretty mind boggling, isn’t it?

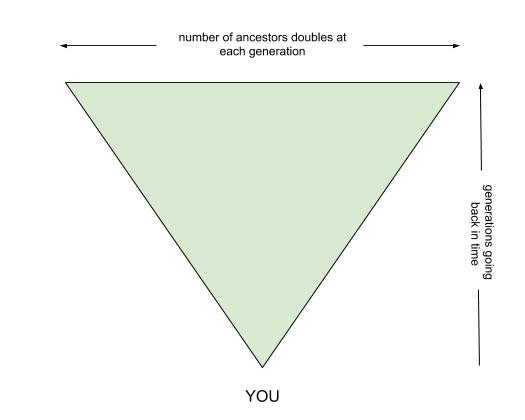
At some point in everyone’s pedigree, instead of different individuals filling out your chain of generations, some of the same ancestors will start to appear multiple times. The term pedigree collapse aptly describes this situation, as when repeat ancestors fill in pedigree slots the inverted triangle starts to collapse in on itself and look more like a diamond.

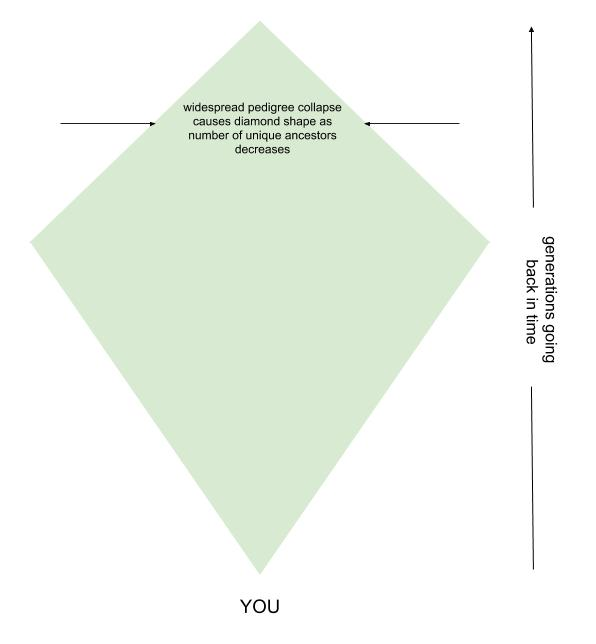
Pedigree collapse and genetic genealogy

Although this scenario plays out in everyone’s pedigree at some point, this becomes relevant to clients of autosomal commercial tests when there is a degree of pedigree collapse in the most recent several generations. This comes into play the most in the client’s match list, where they will see elevated levels of DNA sharing between cousins that descend through the same ancestors that are involved in the pedigree collapse.

Related article and video: Multiple relationships, pedigree collapse or endogamy?

Let’s look at a case study to see just how an instance of pedigree collapse effects levels of DNA sharing between distant cousins. This example examines the question of whether an isolated incident of recent pedigree collapse would raise the amount of DNA shared by downstream cousins enough to send up the red flag. Would this elevated figure tip them off that there is likely an incident of isolated pedigree collapse in their recent ancestry? Or perhaps the level of DNA sharing might still fall in the expected range for their degree of relationship?

Meet the Colapso family. Patriarch and matriarch, Adam and Anna have two children, Bob and Betsy. These siblings marry spouses that are unrelated to the Colapso family and have their own children, Charlie and Cindy who are first cousins. Things start to get interesting when these first cousins marry and have two children, Dan and Diane.

Looking first at Dan, he has 2 parents as we’d expect, and 4 grandparents, but instead of the expected 8 different great-grandparents he has only 6 unique great-grandparents. He is related to Adam and Anna through both his dad and his mom. This is also true for Dan’s sister, Diane– she has only 6 great-grandparents and is related to Adam and Anna through both her mom and dad. Can you see the beginnings of the diamond shape of this collapsed pedigree?

Is your family tree optimized for the best possible DNA matching experience? Get our free guide: Is Your Family Tree DNA-Ready? 

Get free guide: DNA-ready family tree

The math of pedigree collapse

To start with, we are going to focus first on the DNA contributions of the patriarch and matriarch, Adam and Anna, and how they are propagated through the generations of their family. Charlie and Cindy are also common ancestors of the further downstream descendants and we will address this soon, but for now we will just focus on the DNA dissemination of Adam and Anna.

Going back to Dan and Diane, we can see that they are siblings, of course. But relative to their great-grandparents, Adam and Anna, they are also 2nd cousins and are related to them through both their mom and dad. Siblings and 2nd cousins simultaneously: tricky, yes? With Adam and Anna as the reference point, Dan and Diane’s children are 3rd cousins, and the next generation of children are 4th cousins.

In pedigrees both with and without collapse, there is an expected average level of DNA sharing that can be calculated given what we know about genetic inheritance. We expect increased levels of DNA sharing between cousins whose pedigrees are collapsed, and it’s instructive to look at the actual numbers for comparison. We’re going to start to get “math-y” now, but hang in there with me. It’s fun.

On average, children inherit 50% of their DNA each from their mom and dad, 25% from each of their 4 grandparents, 12.5% from each of their 8 grandparents, 6.25% from each of their 16 great-grandparents, and so forth. The average amount of DNA inherited from an individual ancestor is halved going back each generation level beginning with the parents. It’s important to note that these are just averages and the actual amount of DNA inherited is random but will fall in a range around the average numbers.

It’s also important to note that due to random inheritance, the further back the ancestor the less likely that there are segments large enough in current descendants today to be detected by the types of markers and methods currently used by ancestry testing companies. For instance, AncestryDNA estimates that only 32% of documented fifth cousins will share enough DNA inherited from their common ancestor for that relationship to be detected.

Further developing this idea, cousins inherit a predictable amount of DNA from their ancestor, but they don’t necessarily inherit the same segments of DNA. For instance, 1st cousins will inherit on average 25% of DNA from one of their common grandparents, but it is expected that on average they will only inherit 6.25% of the same DNA (that’s 25% of the 25%). Here’s how some of these numbers play out through the generations of inheritance.

Coefficient of relationship in genetic family trees

A term that has been used by geneticists for a long time that quantifies the expected amount of shared DNA between related individuals is called the coefficient of relationship. It’s a great choice to use as a lens for deciphering genetic relationships in the presence of pedigree collapse, or other confounding factors, as it systematically breaks the pedigree down into component parts and analyzes them one by one. Let’s look at how it works through several generations of a pedigree without collapse, and then apply it to the Colapso family example.

The important elements of the coefficient of relationship are (1) identifying the distinct inheritance pathways that exist between the people of interest, and (2) the degrees of relationship that separate them along those distinct pathways. Note that each relationship path must be independent, with each individual appearing in the same pathway only once.

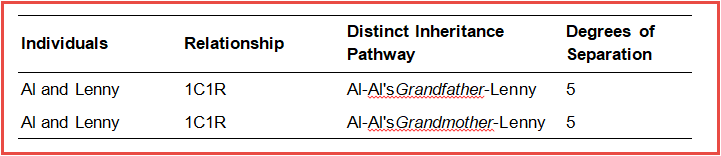
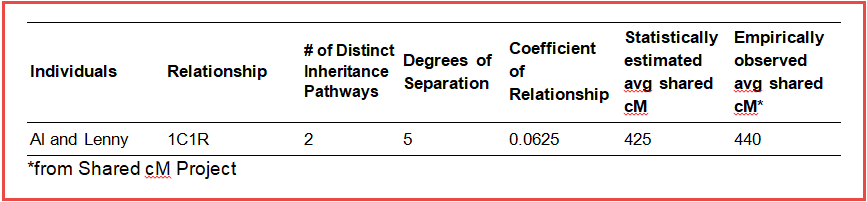
This pedigree describes how Today Show weatherman Al Roker and super-cool rocker Lenny Kravitz are related. We will use this pedigree to determine their coefficient of relationship.

Al’s 1st cousin is Lenny’s mom, making Al and Lenny 1st cousins once removed. From this diagram we can determine both (1) the distinct inheritance pathways that exist between them, and (2) the degrees of relationship that separate them along those distinct pathways. Al and Lenny receive DNA from both Al’s grandfather and Al’s grandmother, so these mark the two distinct inheritance pathways through which Al and Lenny received their DNA from their common ancestors.

Focusing first on the pathway through Al’s grandfather, there are 2 steps up from Al and then 3 steps down to Lenny, making 5 degrees of relationship between Al and Lenny. For the distinct inheritance pathway through Al’s grandmother, similarly there are also 5 degrees of relationship that separate them.

The coefficient of relationship utilizes the idea that with each degree of separation, the amount of DNA that is transmitted to the new generation is reduced by ½, as we explored above. It also takes into account that each distinct inheritance pathway contributes that predictable average amount of DNA to the descendants of interest, and those amounts can be summed together to give a numerical representation of how closely related two people are.

­­For Al and Lenny, let’s apply the numbers we determined earlier for degrees of relationship through their two distinct inheritance pathways.

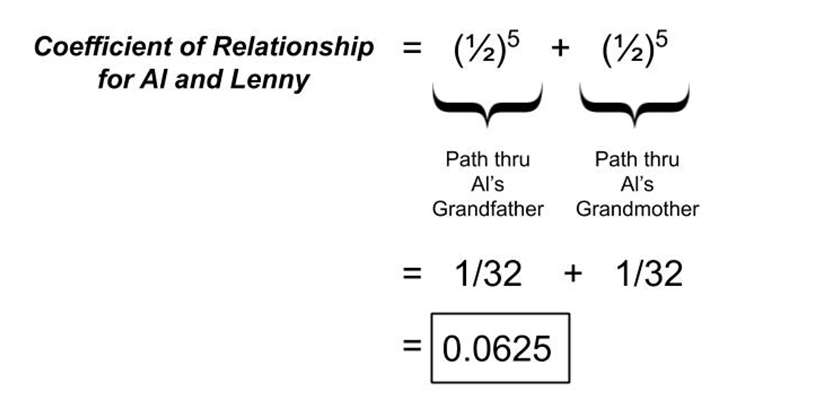
This means that it is predicted on average that Al and Lenny will share 6.25% of their DNA. Although there is no absolute conversion from this percentage of shared DNA to the number of shared centimorgans, some use 6800 cM of total inherited autosomal DNA as a reference point for approximating shared cM.

6.25% x 6800 cM = 425 cM

Data from the Shared cM Project, which has compiled observed levels of cM sharing for thousands of relationship pairs, is also a great reference for comparison of expected DNA sharing between relatives. The average for 1C1R, 440 cM (with an observed range of 235-665 cM), comfortably corroborates  the 425 cM number we estimated statistically.

Using this statistical method for estimating shared DNA for Al Roker and Lenny Kravitz within their non-collapsed pedigree, we have been able to determine some useful measures that describe their genealogical and genetic relationship.

There’s more! Read the second half of this article for calculations and scenarios to apply to your own research.